Acerca de la demostración en Geometría

¿Tienes problemas con las demostraciones?

¿No sabes por qué hay que demostrar?

¿No sabes como realizar una demostración?

¿Tu demostración quedó ordinaria y todos la criticaron?

Este es el libro que necesitas, si TU… yo sé que debes leerlo… y todos nosotros los sabemos, así que es tu oportunidad de descargarlo leerlo y aplicarlo.

Titulo: Acerca de la demostración en Geometría

Autor: A. I. Fetisov

Editorial: MIR

Idioma: Español

Formato: PDF

Descargar aquí (o en la imagen)

Pass: underground69

Challenging Problems In Geometry

¿El poder del ocio se ha apoderado de ti? pues aquí te traigo la solución!!!

Es una colección cientos de problemas inusuales para recrearse en esas tardes de ocio extremo, además se sermuy útil para obtener nuevas ideas y acercarse a la dificultad de problemas olímpicos de geometría. Separado en secciones congruencia y paralelismo, teorema de Pitagoras, círculos, relaciones de area, Ptolomeo y los cuadrilateros cíclicos, colinealidad y concurrencia, entre otros. Lo mejor es que están ordenados en orden de dificultad y con sus soluciones. Altamente recomendado para aquellos principiantes y también a los ya experimentados.

Título: Challenging Problems In Geometry.djvu

Autor: A.S. Posamentier – C.T. Salkind

Idioma: Ingles

Formato: DjVu (mi favorito)

Pass: underground69

Descargar : AQUÍ! (o en la imagen)

Pack ensayos PSU Cpech

La verdad que al revisar estos ensayos, me encontré con algunos ejercicios mal planteados y una que otra respuesta con alternativas incorrectas, pero nunca está de más tener algo de material para entregar y ejercitar.

Es un pack de 16 ensayos con sus respectivas claves, espero tener a futuro acceso a nuevos ensayos de este «prestigioso» preuniversitario, para ponerlos a su disposición lo antes posible.

Hospedaje: MediaFire

Descarga

P.D: Les recomiendo revisar antes de usar, no se confíen con este material, porque tiene algunas fallas.

Compilado Ensayos PSU

Para hoy he preparado un pequeño compilado de ensayos con pruebas que he encontrado por aquí y por allá.

Son 11 archivos con distinta cantidad de preguntas y de distinta calidad en su elaboración, pero nunca está de más tener algo de material extra para la preparación de tu Prueba o tu Preuniversitario.

Espero les guste y les sea de mucha utilidad

Hospedaje: MediaFire

Descarga

Demostración Teorema de Pitágoras por Euclides

Leyendo una de las recientes entradas que realizó nuestro colega Underground69 acerca del libro de los elementos de Euclides, me dio la intriga si encontraba en alguna parte la demostración que hace éste acerca del teorema de Pitágoras, el archiconocido .

Bueno, navegando llegué a otra página dedicada también a las matemáticas de la cual extraje esta demostración, les animo a que analicen y saquen conclusiones. Asi que antes de que se den la lata de navegar y buscar en otras partes esta demostración, se las traigo ahora de mano de esta pagina española

«El texto de matemáticas de mayor éxito que se haya escrito nunca es sin duda los Elementos de Euclides. Se trataba de un libro de texto que no era, como se piensa a veces, un compendio de todos los conocimientos geométricos, sino más bien un texto introductorio que cubría toda la matemática elemental.

Los Elementos están divididos en trece libros o capítulos, de los cuales la primera media docena son de geometría plana elemental, los tres siguientes de teoría de números, el libro X de los inconmensurables y los tres últimos, principalmente, de geometría de sólidos. Los Elementos de Euclides no solamente fueron la primera obra matemática griega de importancia que ha llegado hasta nosotros, sino también el libro de texto que ha ejercido una mayor influencia en todos los tiempos.

Fue escrito hacia el 300 a.C. y desde entonces fue copiado y recopiado sin cesar, con la consecuencia de que se deslizaron en él errores y variaciones de una manera inevitable. Sin embargo, ha sido posible obtener una impresión bastante buena del contenido de la versión euclídea por comparación entre más de media docena de copias griegas manuscritas que datan en su mayoría de entre los siglos X y XII. La primera versión impresa de los Elementos apareció en Venecia en 1.482, y fue uno de los primerísimos libros matemáticos que se imprimió; se estima que desde entonces se han publicado más de un millar de ediciones. Probablemente ningún otro libro salvo la Biblia puede jactarse de haber tenido tantas ediciones y desde luego ninguna otra obra matemática ha tenido una influencia comparable con la de los Elementos de Euclides.

La mayor parte de las proposiciones del Libro I de los Elementos de Euclides son bien conocidas. Entre ellas están los conocidos teoremas sobre las construcciones elementales con regla y compás, sobre las desigualdades relativas a ángulos y lados de un triángulo, sobre las propiedades de las rectas paralelas (con la consecuencia principal de que la suma de los ángulos de un triángulo es igual a dos ángulos rectos) y de los paralelogramos.

El libro concluye en las proposiciones 47 y 48 con las demostraciones del teorema de Pitágoras y su recíproco. La demostración que da Euclides no es la que se da normalmente en los libros de texto actuales, en los cuales se aplican proporciones simples entre los lados de los triángulos semejantes que se forman al trazar la altura correspondiente a la hipotenusa. Se supone que Euclides evitó esta demostración debido a las dificultades que trae consigo en el caso de inconmensurabilidad.

Para demostrar el teorema de Pitágoras, Euclides utilizó en cambio una bella demostración en la que se usa una figura que se ha descrito a veces como un molino de viento o como una cola de pavo real o bien como la Silla de la Novia.

La demostración viene a ser la siguiente:

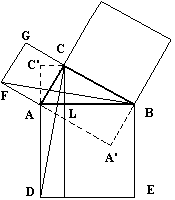
• El área del triángulo AFB es , y como resulta que

• El área del triángulo BCD es 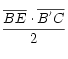, y como 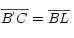resulta que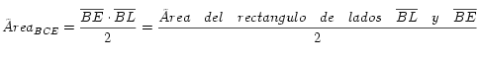

• Y como fácilmente se ve que los triángulos AFB y ACD son iguales

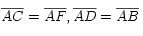(y el ángulo determinado por estos lados es el mismo), obtenemos que el área del cuadrado de lado 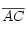es igual al área del rectángulo de lados 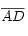y .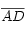

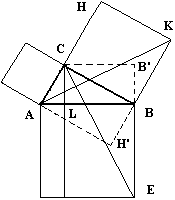o si pudieramos verlo mejor…

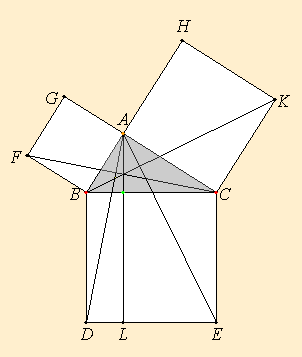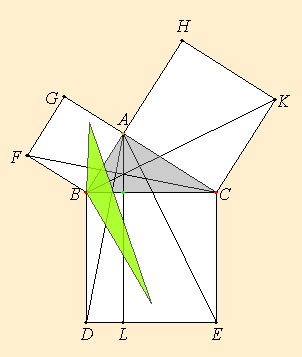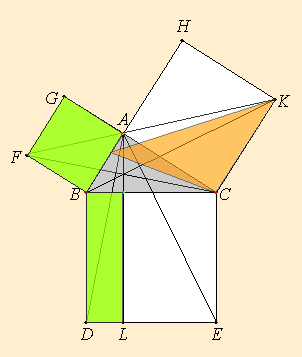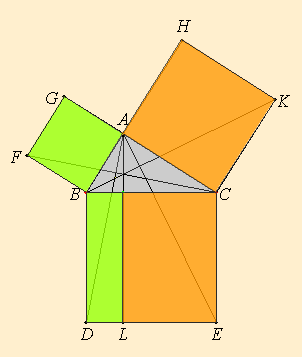Este diagrama animado muestra la demostración de Euclides como una dinámica de modificaciones sucesivas de triángulos equivalentes.

Luego:

• El área del triángulo ABK es 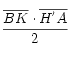, y como 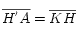resulta que
• El área del triángulo BCE es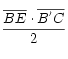, y como 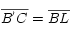resulta que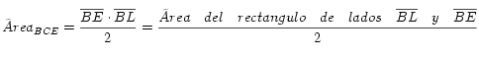
• Y como fácilmente se ve que los triángulos ABK y BCE son iguales ( 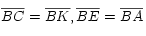y el ángulo determinado por estos lados es el mismo), obtenemos que el área del cuadrado de lado 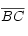es igual al área del rectángulo de lados 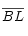y .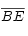

En definitiva, hemos demostrado que la suma de las áreas de los cuadrados de lados los catetos del triángulo rectángulo ABC, es igual al área del cuadrado de lado la hipotenusa de dicho triángulo rectángulo. O sea, que la suma de los cuadrados de los catetos del triángulo rectángulo ABC es igual al cuadrado de la hipotenusa de dicho triángulo rectángulo: AB²=AC²+CB².

Se supone que esta demostración es original de Euclides y se han hecho muchas conjeturas acerca de la forma que ofrecerían las demostraciones anteriores.

A partir de la época de Euclides se han propuesto una infinidad de demostraciones alternativas. Es de notar, a cuenta de los méritos de Euclides, el que el teorema de Pitágoras vaya seguido inmediatamente por una demostración del recíproco: si en un triángulo el cuadrado construido sobre uno de los lados es igual a la suma de los cuadrados sobre los otros dos lados, entonces el ángulo que forman estos otros dos lados es un ángulo recto. Es frecuente en algunos libros de textos modernos que los ejercicios que siguen al teorema de Pitágoras requieran no el teorema propiamente dicho, sino el recíproco no demostrado aún.

Puede haber muchos defectos menores en los Elementos, pero el libro tiene todas las virtudes lógicas mayores.

• Demostración del Teorema de Pitágoras utilizando la proporcionalidad entre los lados de los triángulos semejantes que se forman al trazar la altura correspondiente a la hipotenusa:

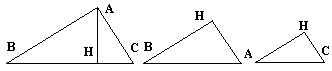
Los triángulos BAC y BHA son semejantes pues tienen un ángulo agudo igual, B. Entonces sus lados homólogos son proporcionales y se cumple que 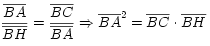(es el Teorema del Cateto).

Los triángulos BAC y AHC son semejantes pues tienen un ángulo agudo igual, C. Entonces sus lados homólogos son proporcionales y se cumple que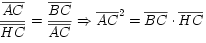(es el Teorema del Cateto referido al otro cateto).

Sumando las dos igualdades anteriores y operando tenemos el Teorema de Pitágoras: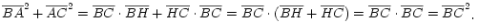

• Veamos ahora una demostración gráfica del Teorema de Pitágoras:

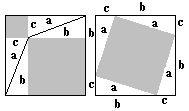
Los dos cuadrados grandes son iguales ya que tienen el mismo lado b + c, y cada uno tiene en su interior cuatro triángulos rectángulos iguales, de lados a (hipotenusa), b y c. Los dos cuadrados sombreados que aparecen en la figura de la izquierda tienen una superficie de b² y c², respectivamente. El cuadrado sombreado que se representa en la figura de la derecha tiene por área a². Las áreas sombreadas que aparecen en las figuras 1 y 2 son iguales, ya que corresponden al área del cuadrado grande menos el área de los cuatro triángulos. Por tanto, tenemos el teorema de Pitágoras: a²=b²+c².